How to Address Increased Loads in Both Size and Weight with a Stepper Motor
Increasing the size and weight will increase the inertia of the load and the torque required to move the load. Gearing is a great option for overcoming large inertia loads as it will decrease the reflected inertia on the motor by the gear ratio squared.
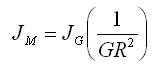
Adding a gear ratio will also increase the amount of torque generated. Typically, the torque produced is equal to the motor torque multiplied by the gear ratio and the efficiency of the gear. However, there are instances when the output torque is limited based on other mechanical reasons, such as gear teeth strength, gear case strength, or gear carrier strength.
Tg = Tm x GR x efficiency
There are multiple gear options available for use. The decision on which gear to use will come down to torque, speed, and backlash requirements. A summary of each gear type is listed below.
In order to make the quickest move possible, acceleration torque must be considered. The more torque available to accelerate, the quicker the move can be made. When comparing gears, planetary gears will have more available torque than taper hobbed or spur gears. This is due to the fact that planetary gears can disperse the force among all of the planetary gears versus each gear taking the entire force. Therefore, planetary gears will be able to make the move quicker than taper hobbed or spur gears.
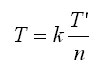
T: Torque applied to each planetary gear (Nm)
T’: Total torque transference (Nm)
n: Number of planetary gears
k: Dispersion coefficient
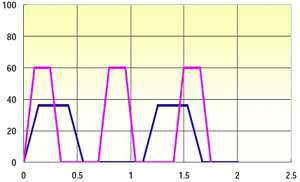
Below is an example on how greater available torque allows for faster acceleration. The taper hobbed gear and the PS planetary gear are used with the 60mm motor in the example.
- Maximum torque
- 60mm TH: 35 lb-in
- 60mm PS: 177 lb-in
- More torque available means that we can accelerate the motor harder, decreasing the move time.
How to Address Increased Loads in Both Size and Weight
- Disk
- 20 inch diameter
- 20 lbs
- Motion Profile
- 360° in 1.5 se
- One direction of motion (CW)
- Safety Factor
- 1.5 minimum
- System Requirements
- Single phase 115 VAC
- Motor and driver needed

In order to keep the load inertia to rotor inertia ratio below 10:1, a gear ratio of at least 40.8 must be used. This eliminates taper hobbed and spur gears from possible solutions. Since the motion only goes clockwise, backlash is not a concern, so we will take a look at the 50:1 PS planetary gear.

The 50:1 planetary gear has a maximum speed of 60 RPM, so this is still an option.


The load torque calculated above is based on a 0.05 coefficient of friction, a 1” distance from the center of the table to the support mechanism, and a 90% overall system efficiency.

The required torque is 1092 oz-in or 68.25 lb-in.